วีดีโอประกอบคำอธิบาย
นวัตกรรมและเทคโนโลยีสารสนเทศเพื่อการศึกษา
วันอังคารที่ 6 ตุลาคม พ.ศ. 2558
วันพฤหัสบดีที่ 1 ตุลาคม พ.ศ. 2558
วันพฤหัสบดีที่ 27 สิงหาคม พ.ศ. 2558
วันอังคารที่ 25 สิงหาคม พ.ศ. 2558
วันพฤหัสบดีที่ 20 สิงหาคม พ.ศ. 2558
เทคนิคการสอนคณิตศาสตร์
เทคนิคการสอนวิชาคณิตศาสตร์
 |
| ที่มาภาพ http://i1243.photobucket.com/albums/gg553/553070068-5/maths.jpg |
วิธีการสอนในการจัดการเรียนการสอนถ้าครูใช้วิธีการสอนที่เหมาะสมกับวิธีการเรียนของผู้เรียนแล้ว จะทำให้การเรียนรู้ของผู้เรียนเป็นไปอย่างมีประสิทธิภาพ และคงทนยั่งยืน ถ้าผู้เรียนได้รับการสอนที่สอดคล้องกับวิธีการเรียนที่ตนชอบ จะทำให้ผลสัมฤทธิ์ทางการเรียนสูงขึ้น มีทัศนคติที่ดีต่อการสอน และมีวินัยในตนเอง สำหรับวิธีการสอนของครูมีการแบ่งได้หลายแบบ แต่จะนำเสนอเฉพาะวิธีที่น่าสนใจ ดังนี้
วิธีสอนคณิตศาสตร์ ที่ทำให้นักเรียนมีผลสัมฤทธิ์ทางการเรียนสูงกว่าวิธีสอนตามปกติ ได้แก่ 1) วิธีสอนแบบวรรณี 2) วิธีสอนโดยใช้สถานการณ์จำลอง 3) วิธีสอนซ่อมเสริมโดยใช้ชุดการสอน บทเรียนโปรแกรม 4) วิธีสอนซ่อมเสริมโดยใช้เกมประกอบการสอน คอมพิวเตอร์ช่วยสอน ชุดฝึกทักษะการคิดคำนวณ และชุดการสอน 5) วิธีสอนรายบุคคลที่ช่วยให้นักเรียนมีผลการเรียน เจตคติต่อการเรียน และความคงทนของการ เรียนรู้สูงที่สุดและสูงกว่าวิธีสอนแบบใช้สื่อการเรียนการสอน วิธีสอนแบบใช้สื่อการเรียนการสอน วิธีสอนแบบนักเรียนเป็นศูนย์กลาง และวิธีสอนแบบครูและนักเรียนมีกิจกรรมร่วมกัน 6)รูปแบบการเรียนการสอนที่ทำให้นักเรียนเกิดการเรียนรู้ตามจุดมุ่งหมายของการเรียนการสอนคณิตศาสตร์ คือรูปแบบการเรียนการสอนที่เน้นทักษะการคิดคำนวณ ที่ยึดหลักทฤษฎีกระบวนการกลุ่มที่มุ่งพัฒนาให้ผู้เรียนเกิดการเรียนรู้ มีความรู้ความเข้าใจในมโนมติ มีทักษะทางคณิตศาสตร์ รู้จักแก้ปัญหาและนำความรู้ไปใช้ในชีวิตประจำวัน รวมทั้งให้นักเรียนมีเจตคติที่ดีต่อวิชาคณิตศาสตร์ และเห็นความสำคัญและความจำเป็นของการคิดคำนวณ 7) รูปแบบการสอนแก้โจทย์ปัญหาคณิตศาสตร์ที่เน้นการคิดแบบอเนกนัย เรื่อง การบวก ลบ คูณทศนิยม และบทประยุกต์ ชั้น ป.5 มีผลสัมฤทธิ์ทางการเรียนสูงกว่าเกณฑ์ความรอบรู้ที่กำหนดร้อยละ 70 และนักเรียนมีคุณลักษณะที่พึงประสงค์ ได้แก่ ทักษะการร่วมอภิปราย การระดมความคิด การยอมรับฟังความคิดเห็นของผู้อื่น ทักษะการทำงานย่อย และการกล้าแสดงออก 8) รูปแบบการสอนแบบร่วมมือกันเรียนรู้ เรื่อง เศษส่วน ทำให้นักเรียนชั้น ป.5 มีผลสัมฤทธิ์ทางการเรียนสูงขึ้น มีเจตคติที่ดีต่อคณิตศาสตร์ และมีทักษะทางคณิตศาสตร์สูงขึ้นแล้วยังเป็นการพัฒนาทักษะทางด้านสังคม ส่งเสริมความสามัคคีของนักเรียน ทำให้นักเรียนมีความมั่นใจและตระหนักในคุณค่าของตนเองมากขึ้น 9) รูปแบบการสอนคณิตศาสตร์ที่เน้นประสบการณ์ทางภาษาของนักเรียน เรื่องการบวก ลบจำนวนที่มีสองหลักและการบวกระคน ทำให้นักเรียนชั้น ป.1 มีผลสัมฤทธิ์ทางการเรียนเฉลี่ยร้อยละ 88.99 และความสามารถในการพัฒนามโนมติทางคณิตศาสตร์เฉลี่ยร้อยละ 85.36 ซึ่งสูงกว่าเกณฑ์ที่กำหนดไม่น้อยกว่าร้อยละ 70 10) รูปแบบการสอนที่เน้นเทคนิควิธีการคิดทางคณิตศาสตร์ เรื่อง เศษส่วน ทำให้นักเรียนชั้น ป. 5 มีผลสัมฤทธิ์ทางการเรียนสู่งกว่าวิธีการสอนตามคู่มือครู
วิธีสอนคณิตศาสตร์ที่น่าสนใจ 11 วิธี
1.วิธีการสอนตามคู่มือ สสวท.
ขั้นตอนการสอน มี 5 ขั้นตอน ได้แก่
1)ขั้นนำ
– ทบทวนความรู้เดิม
2) ขั้นสอน
สอนเนื้อหาใหม่ โดย
– ใช้สื่อประกอบของจริง รูปภาพ สัญลักษณ์
– ใช้กิจกรรมเพลง เกม
– ใช้กิจกรรมเสริม เช่น การจัดป้านนิเทศในชั้นเรียน
– ตรวจสอบความเข้าใจของผู้เรียน ถ้าไม่เข้าใจก็ทบทวนหรือสอนใหม่ ถ้าเข้าใจจึงผ่านไปขั้นสรุปต่อไป
3) ขั้นสรุป
– สรุปเป็นวิธีลัด หรือความคิดรวบยอด
4)ขั้นฝึกทักษะ
– ทำแบบฝึกหัดในหนังสือเรียน บัตรงาน
5)ขั้นประเมินผล
– ตรวจสอบผลการเรียนและการนำไปใช้ ถ้าไม่ผ่านก็จัดสอนซ่อมเสริม ถ้าผ่านก็สอนเนื้อหาใหม่ต่อไป
2.วิธีสอนตามหลักของโพลยา เรื่องที่สอน จะนิยมใช้ในการแก้โจทย์ปัญหาคณิตศาสตร์ ขั้นตอนการสอน มี 4 ขั้นตอน ได้แก่ 1) ทำความเข้าใจปัญหา ขั้นตอนนี้ครูมีบทบาทสำคัญมาก ครูจะต้องทำหน้าที่ตั้งคำถามนำเพื่อให้ผู้เรียนเข้าใจโจทย์ข้อนั้น ๆ อย่างถูกต้อง ตัวอย่างคำถาม เช่น โจทย์บอกอะไรมาให้เรารู้บ้าง โจทย์ต้องการรู้อะไร โจทย์ต้องการให้เราทำอะไร ผู้เรียนสามารถพูดเกี่ยวกับโจทย์เป็นคำพูดของตัวเองได้หรือไม่ โจทย์ข้อนี้ผู้เรียนจะวาดรูปเพื่อให้เข้าใจง่าย ๆ หรือไม่ เป็นต้น 2) วางแผนในการแก้ปัญหา ขั้นตอนนี้ครูจะแสดงบทบาทไปพร้อม ๆ กับผู้เรียน ร่วมกันวางแผนเพื่อแก้ปัญหาโจทย์ อาจมีคำถามนำเพื่อวางแผน เช่น ผู้เรียนเคยแก้โจทย์ปัญหาที่คล้าย ๆ กับโจทย์ข้อนี้ไหม ผู้เรียนคิดว่าโจทย์ข้อนี้ควรทำอย่างไร 3) ลงมือทำตามแผน ขั้นตอนนี้ผู้เรียนจะลงมือคำนวณตามแนวทางที่จัดไว้ในขั้นตอนที่ 2 4) ตรวจวิธีการและคำตอบ เป็นขั้นตอนของการตรวจสอบความถูกต้องของการคิดคำนวณ การลงความเห็นหรือสรุปเป็นหลักการของการคำนวณ 3.วิธีสอนแบบวรรณี ขั้นตอนการสอน 1)ขั้นนำ – เร้าความสนใจ – ฝึกสมาธิ – ทบทวนพื้นความรู้เดิม 2) ขั้นสอน สอนเนื้อหาใหม่โดยใช้ –กิจกรรมให้เข้าใจโดยใช้ของจริง ของจำลอง ภาพ สัญลักษณ์ –กิจกรรมเสริมความเข้าใจโดยใช้ภาพ สัญลักษณ์ – กิจกรรมเสริมสร้างเจตคติโดยใช้สถานการณ์ หรือเกม การแข่งขัน 3)ขั้นสรุป – สรุปความเข้าใจ – สรุปวิธีลัด – สรุปวิธีแก้ปัญหา 4)ขั้นฝึกทักษะ – ทำแบบฝึกหัด บัตรงาน 5) ขั้นนำไปใช้ – ฝึกแก้โจทย์ปัญหาตามสถานการณ์ – ส่งเสริมการนำไปใช้ในชีวิตประจำวัน 6)ขั้นประเมินผล – สังเกตการณ์ตอบคำถาม การทำกิจกรรม – ตรวจแบบฝึกหัด – ทดสอบย่อยตามจุดประสงค์ 4.วิธีสอนแบบทักษะกระบวนการ แนวคิดในการสอน ยึดหลักปรัชญาการศึกษาแบบพิพัฒนาการ (Progressivism) โดยเน้นผู้เรียนเป็นศูนย์กลาง ขั้นตอนการสอน มี 3 ขั้นตอน ได้แก่ 1) ให้นักเรียนฝึกทักษะการท่องสูตรคูณเร็ว 2) ครูนำโจทย์ปัญหาให้ผู้เรียนฝึกวิเคราะห์ แล้วเขียนเป็นประโยคสัญลักษณ์ และหาคำตอบ 3) ครูและผู้เรียนช่วยกันสรุปเกี่ยวกับการวิเคราะห์โจทย์ปัญหา
5. วิธีสอนแบบเล่นปนเรียน ขั้นตอนการสอน มี 5 ขั้นตอน ได้แก่ 1) ขั้นนำเข้าสู่บทเรียน – ใช้เพลง เกม หรือการแข่งขันคิดเลขเร็ว 2)ขั้นสอน – ทดสอบความรู้พื้นฐานที่สัมพันธ์กับเนื้อหาที่จะเรียนต่อไป – อธิบายทบทวนพื้นความรู้เดิมก่อน – สอนเนื้อหาใหม่ โดยใช้ภาพ สื่ออื่น ๆ ประกอบคำอธิบายทีละขั้นตอน – ยกตัวอย่างวิธีทำ ถามผู้เรียนทีละคน ให้ช่วยกันคิดหาวิธีทำ จนเข้าใจแล้วแนะเทคนิควิธีคิดที่ง่าย ๆ แนะข้อผิดพลาดที่ผู้เรียนมักทำผิดหรือเข้าใจผิด – ให้ผู้เรียนยกตัวอย่างโจทย์เอง และช่วยกันติดบนกระดานก่อนที่จะทำแบบฝึกหัด 3)ขั้นสรุปบทเรียน – ให้แข่งขันกันคิดเลขด้วยเม หรือคิดเลขเร็ว 4)ขั้นฝึกทักษะ – ให้ทำแบบฝึกหัดตามตัวอย่าง ครูเดินตรวจทีละคน หากพบผู้เรียนที่ทำไมได้ ให้อธิบายทันทีก่อนให้การบ้าน 5)ขั้นประเมินผล – เมื่อจบบทเรียนให้วัดมาตรฐานตัวชี้วัด 6. วิธีสอนสอดแทรกการฝึกทักษะการคิดคำนวณ 6.1 รูปแบบที่ 1 : ขั้นตอนการสอน มี 3 ขั้นตอน ได้แก่ ก่อนหรือหลังเรียนคณิตศาสตร์ในแต่ละวัน ครูใช้เวลา 5-10 นาที ห้ผู้เรียนฝึกทักษะการคิดคำนวณกิจกรรมทีใช้ คือ 1)ฝึกการท่องสูตรคูณทุกครั้งที่มีการเรียนคณิตศาสตร์ 2) ฝึกการคิดเลขเร็ว (ประมาณ 5 – 10 นาที) ทุกครั้งที่มีการเรียนคณิตศาสตร์ โดยใช้แบบทดสอบ/แบบฝึกที่ครูสร้างขึ้น 3)ฝึกการวิเคราะห์โจทย์ปัญหาทุกวัน อย่างน้อยวันละ 1 ข้อ 6.2รูปแบบที่ 2 ขั้นตอนการสอน มี 3 ขั้นตอน ได้แก่ 1) ย้ำ 2) ซ้ำ 3) ทวน 7. วิธีสอนแบบอุปนัย (Inductive Method) การสอนแบบอุปนัย หมายถึง การสอนจากส่วนย่อยไปหาส่วนใหญ่ หรือจากตัวอย่างไปหาข้อสรุป หรือกฎเกณฑ์ ขั้นตอนการสอน มี 3 ขั้นตอน ได้แก่ 1)ขั้นเตรียม เป็นขั้นที่ครูทบทวนความรู้เดิมและเร้าความสนใจของผู้เรียน ครูอาจจะเล่าเรื่อง ใช้อุปกรณ์ ตั้งคำถาม 2) ขั้นสอน ครูให้ผู้เรียนดูตัวอย่างประกอบหลาย ๆ ตัวอย่าง เพื่อให้ผู้เรียนสังเกต 3) ขั้นเปรียบเทียบ ครูให้ผู้เรียนเปรียบเทียบตัวอย่างในขั้นที่ 2 ว่ามีความแตกต่างและคล้ายคลึง หรือมีความสัมพันธ์กันอย่างไรบาง ในข้นนี้ผู้เรียนอาจมีการทดลอง วิเคราะห์ผลจากการสังเกตหรือทดลอง 8. วิธีสอนแบบนิรนัย (Deductive Method) การสอนแบบนิรนัย หมายถึง การสอนที่ให้ผู้เรียนรู้หลักเกณฑ์หรือข้อเท็จจริงเสียก่อน แล้วจึงให้เรียนข้อเท็จจริงปลีกย่อย หรืออีกนัยหนึ่งก็คือการสอนจากกฎไปหาตัวอย่างที่เป็นรายละเอียด ขั้นตอนการสอน มี 4 ขั้นตอน ได้แก่ 1) อธิบายปัญหา (Statement of Problem) ครูอธิบายว่าอะไรคือปัญหาและปัญหานั้นมีความสำคัญอย่างไร 2)การสรุปนัยทั่วไป (Generalization ) ครูแนะนำและอธิบายกฎ สูตร นิยาม ความจำเป็นต้องนำมาใช้แก้ปัญหานั้น 3)อนุมาน ( Inference ) นักเรียนเป็นผู้พิจารณาคัดเลือกการใช้กฎเกณฑ์หรือสูตร หรือนิยามมาใช้เพื่อแก้ปัญหา 4)ตรวจสอบพิสูจน์ (Verfication ) เมื่อนักเรียนนำกฎหรือสูตรหรือนิยามมาใช้แล้ว นักเรียนจะต้องตรวจสอบอีกครั้งหนึ่งว่าถูกต้องหรือไม่ ในขั้นนี้อาจมีการค้นคว้าจากหนังสือหรือเอกสารหรือหลักฐานต่าง ๆ 9.วิธีสอนแบบสาธิต ( Demonstration ) การสอนแบบสาธิต หมายถึง การสอนที่ดำเนินการโดยครูเป็นผู้กำหนดปัญหา และแสดงวิธีการหาคำตอบ ผู้เรียนเป็นผู้ปฏิบัติตาม หากครูอธิบายได้ดีจะเป็นวิธีที่ประหยัดเวลา ขั้นตอนการสอน มี 3 ขั้นตอน ดังนี้ ขั้นที่ 1 บอกความคิดรวบยอด ครูเป็นผู้กำหนดเรื่องที่จะสอนและบอกความคิดรวบยอดของเรื่องที่จะสอน เช่น ตัวประกอบของจำนวนนับใด ๆ คือ จำนวนนับที่หารจำนวนนั้นได้ลงตัว ขั้นที่ 2 เสนอตัวอย่าง ครูแสดงตัวอย่างให้ผู้เรียนดูหลาย ๆ ตัวอย่าง เช่น 36 ÷ 6 = 6 , 45 ÷ 9 = 5 , 56 ÷ 7 = 8 ฯลฯ และครูแสดงจำนวนที่หารไม่ลงตัว เช่น 27 ÷ 6 = 4 เศษ 3 , 41 ÷ 8 = 5 เศษ 1 , 58 ÷ 7 = 8 เศษ 2 ฯลฯ พร้อมทั้งสรุปได้ความคิดรวบยอดตามที่กำหนดไว้ว่า จำนวนที่หารจำนวนใดลงตัวก็เป็นตัวประกอบของจำนวนนั้น ในการสอนระหว่างขั้นที่ 1 บอกความคิดรวบยอด และขั้นที่ 2 เสนอตัวอย่างอาจสลับขั้นกันได้ บางครั้งอาจเสนอตัวอย่างก่อนแล้วจึงสรุปความคิดรวบยอด ขั้นที่ 3 ฝึกปฏิบัติ ให้ผู้เรียนปฏิบัติโดยแสดงวิธีแก้ปัญหาโจทย์ที่มีความคิดรวบยอดตามที่เรียนไป โดยเรียนรู้จากแนวคิดที่ครูแสดงให้ดู
10.วิธีสอนเพื่อให้เกิดความคิดรวบยอด ( Concept Attainment ) การสอนเพื่อให้เกิดความคิดรวบยอด หมายถึง การสอนที่มุ่งให้ผู้เรียนรู้คุณลักษณะของสิ่งใดสิ่งหนึ่งเรื่องใดเรื่องหนึ่ง หรือเหตุการณ์ใดเหตุการณ์หนึ่ง โดยสามารถระบุลักษณะเด่น ลักษณะรองของสิ่งนั้นได้ สามารถนำความรู้ที่เกิดขึ้นไปใช้ในสถานการณ์อื่น ๆ
ขั้นตอนการสอน มี 5 ขั้นตอน ดังนี้
ขั้นที่ 1 ครูจัดสถานการณ์ให้ผู้เรียนเกิดการเรียนรู้ โดยการนำเสนอเหตุการณ์รายละเอียดของสิ่งต่าง ๆ ให้ผู้เรียนได้รับรู้ สังเกต พิจารณาลักษณะเด่นและลักษณะประกอบของสิ่งนั้นๆ
ขั้นที่ 2 ครูให้ผู้เรียนระบุลักษณะเด่น และลักษณะรองของสิ่งที่ได้สังเกต และหาลักษณะที่เหมือนกันและลักษณะที่แตกต่างกัน
ขั้นที่ 3 ครูให้ผู้เรียนสรุปลักษณะสำคัญที่สังเกตได้ พร้อมกับให้ชื่อของสิ่งนั้น
ขั้นที่ 4 ครูตรวจสอบความเข้าใจของผู้เรียนและความเป็นไปได้ ความเหมาะสมของชื่อ ความคิดรวบยอดนั้น
ขั้นที่ 5 ครูกำหนดสถานการณ์ใหม่ให้ผู้เรียนได้นำความคิดรวบยอดที่เกิดขึ้นไปใช้
11.การสอนโดยใช้เทคนิค KWDL
การสอนโดยใช้เทคนิค KWDL หมายถึง เทคนิคการจัดการเรียนรู้ที่พัฒนาจากเทคนิค KWL ของโอเกิล (Ogle,1986) ที่ต้องอาศัยทักษะการอ่านเป็นพื้นฐาน นั่นคือ นักเรียนต้องมีความสามารถในการอ่านก่อนจึงจะสามารถพัฒนาทักษะการอ่านให้มีคุณภาพมากขึ้นด้วยเทคนิค KWL , KWDL และ KWL plus วิธีการจัดการเรียนรู้โดยใช้เทคนิคหรือกระบวนการ KWDL มีขั้นตอนการดำเนินการเช่นเดียวกับ KWL เพียงแต่เพิ่มขั้น D ในขั้นตอนที่ 3 ซึ่ง KWDL มาจากคำที่ว่า
K : เรารู้อะไร (What we know) หรือโจทย์บอกอะไรเราบ้าง (สำหรับคณิตศาสตร์)
W : เราต้องการรู้ , ต้องการทราบอะไร (What we want to know)
D : เราทำอะไร , อย่างไร (What we do) หรือเรามีวิธีอย่างไรบ้าง หรือมีวิธีดำเนินการเพื่อหาคำตอบอย่างไร
L : เราเรียนรู้อะไรจากการดำเนินการ ขั้นที่ 3 (What we learned) ซึ่งคือคำตอบสาระความรู้ และวิธีหาคำตอบและขั้นตอนการคิดคำนวณ เป็นต้น
แผนภูมิเทคนิคการจัดการเรียนรู้โดยใช้ KWDL
โจทย์ปัญหาคณิตศาสตร์ : KWDL Chart
ขั้นที่ 1 ครูจัดสถานการณ์ให้ผู้เรียนเกิดการเรียนรู้ โดยการนำเสนอเหตุการณ์รายละเอียดของสิ่งต่าง ๆ ให้ผู้เรียนได้รับรู้ สังเกต พิจารณาลักษณะเด่นและลักษณะประกอบของสิ่งนั้นๆ
ขั้นที่ 2 ครูให้ผู้เรียนระบุลักษณะเด่น และลักษณะรองของสิ่งที่ได้สังเกต และหาลักษณะที่เหมือนกันและลักษณะที่แตกต่างกัน
ขั้นที่ 3 ครูให้ผู้เรียนสรุปลักษณะสำคัญที่สังเกตได้ พร้อมกับให้ชื่อของสิ่งนั้น
ขั้นที่ 4 ครูตรวจสอบความเข้าใจของผู้เรียนและความเป็นไปได้ ความเหมาะสมของชื่อ ความคิดรวบยอดนั้น
ขั้นที่ 5 ครูกำหนดสถานการณ์ใหม่ให้ผู้เรียนได้นำความคิดรวบยอดที่เกิดขึ้นไปใช้
K
โจทย์บอกอะไรบ้าง
|
W
โจทย์ให้หาอะไร
|
D
ดำเนินการตามกระบวนการ
|
L
คำตอบที่ได้ และคิดคำตอบอย่างไร
|
……………………….
……………………….
2. ………………
………………………..
|
……………………….
……………………….
2. ………………
…………………..….
| แสดงวิธีทำวิธีที่ 1
ประโยคสัญลักษณ์
……………………….
……………………….
| คำตอบ……………………
สรุปขั้นตอน
……………………
……………………
|
| พี่ชายใจดีมีเงินอยู่ 3,200 บาท แบ่งให้น้อง 5 คน คนละเท่า ๆ กัน น้องแต่ละคนจะได้เงินคนละเท่าไร |
K
โจทย์บอกอะไรบ้าง
|
W
โจทย์ให้หาอะไร
|
D
ดำเนินการตามกระบวนการ
|
L
คำตอบที่ได้ และคิดคำตอบอย่างไร
|
อยู่ 3,200 บาท
2.แบ่งให้น้อง5 คน ๆ ละ เท่า ๆ กัน
| -น้องแต่ละคนจะได้เงินคนละเท่าไร | แสดงวิธีทำวิธีหาร (÷)ประโยคสัญลักษณ์ 3,200÷5=ם
วิธีทำ
พี่ชายใจดีมีเงินอยู่ 3,200 บาท ÷
แบ่งให้น้อง 5 คน
น้องแต่ละคนจะได้เงินคนละ640 บาท
ตอบ 640 บาท
| คำตอบ640 บาท
สรุปขั้นตอน
3,200 ÷5 = 640
|
| K โจทย์บอกอะไรบ้าง | W โจทย์ให้หาอะไร | D ดำเนินการตามกระบวนการ | L คำตอบที่ได้ และคิดคำตอบอย่างไร |
| 1. ……………… ………………………. ………………………. 2.……………… ……………………….. ………………………. | 1.…………………. ………………………. ………………………. 2.………………….. …………………..………………………. | แสดงวิธีทำ วิธีที่ 1……………….. วิธีที่ 2 ……………………. ประโยคสัญลักษณ์ ………………………. ………………………. | คำตอบ……………………
สรุปขั้นตอน
……………………
……………………
……………………
|
ที่มาของข้อมูล https://goo.gl/iLZ2E2
นวัตกรรมทางคณิตศาสตร์
คณิตศาสตร์กับการคิดเลขเร็ว
เด็กนักเรียนเริ่มรู้จักตัวอักษร ก, ข, ... พร้อมกับตัวเลข 1, 2, 3 ... และเรียนรู้วิธีสะกดคำ พร้อมกับการนับเลขซึ่งเป็นพื้นฐานของการคำนวณ ถ้าเด็กสามารถบวกเลข 1 หลักได้ ก็สามารถหาผลบวกของเลขกี่หลักก็ได้ เพราะการบวกเลขหลายหลักใช้วิธีคำนวณทีละหลักแล้วทดไปหลักถัดไป การบวกเลขง่ายกว่าการอ่านหนังสือเพราะตัวเลขมีเพียง 10 ตัว (0-9) นำมาจับคู่บวกกันได้ 10 x 10 = 100 คู่ (เลข 1 หลัก) แต่ตัวอักษร สระ และวรรณยุกต์มีถึง 44 ตัว นำมาผสมเป็นคำศัพท์ต่าง ๆ ได้มากกว่า 100 คำ สิ่งที่น่าประหลาดใจคือ มีนักเรียนจำนวนมากสามารถอ่านหนังสือได้โดยไม่ต้องสะกด แต่ไม่สามารถหาผลบวกได้โดยไม่ต้องนับ การอ่านหนังสือโดยไม่ต้องสะกดเป็นเรื่องสำคัญมากเพราะถ้านักเรียนยังคงต้อง สะกดทุกคำในการอ่าน จะไม่สามารถอ่านตำราเป็นเล่มได้รู้เรื่อง เพราะเสียสมาธิไปกับการสะกด แทนที่จะใช้สมาธิไปกับเนื้อหาที่อ่าน ทักษะการคำนวณก็เช่นกัน หาก นักเรียนต้องใช้สมาธิไปกับการนับเลขเพื่อหาผลลัพธ์จะทำให้เหลือสมาธิสำหรับแก้ปัญหาอื่นน้อยลง |
| คำถามที่น่าสนใจคือ ทำไมนักเรียนสามารถอ่านหนังสือโดยไม่ต้องสะกดได้ แต่ไม่สามารถบวกเลขโดยไม่ต้องนับ ? ทั้งที่ตัวเลขมีเพียง 10 ตัว (0-9) แต่ตัวอักษร สระ และ วรรณยุต์ไทยมีถึง 44 ตัว ผลลัพธ์น่าจะกลับกัน ส่วนหนึ่งเป็นผลมาจากการปลูกฝังความคิดว่าคณิตศาสตร์เป็นเรื่องของความเข้าใจ ขอให้เข้าใจก็พอ ไม่ต้องจำ นักเรียนส่วนใหญ่จึงหยุดพัฒนาทักษะด้านคำนวณ เพราะเมื่อนับแล้วได้คำตอบ ก็แสดงว่าเข้าใจแล้ว ไม่จำเป็นต้องมีทักษะมากไปกว่านี้ นอกจากนี้การใช้เครื่องคิดเลขจนเคยชิน มีส่วนทำให้ทักษะในการคำนวณหดหายไป แต่ในการสอบแข่งขันมักไม่อนุญาตให้ใช้เครื่องคิดเลข เนื้อหาส่วนนี้เป็นการนำเสนอวิธีพัฒนาความเร็วในการบวก ลบ คูณ และหารเลข ซึ่งเป็นทักษะการคำนวณที่จำเป็นอย่างมากในการทำข้อสอบ เนื่องจากทุกสนามสอบมีการจำกัดเวลา นักเรียนต้องคำนวณให้ได้คำตอบที่ถูกต้องก่อนหมดเวลา ดังนั้นผู้ที่สามารถคิดเลขได้เร็วกว่าย่อมได้เปรียบ วิธีสอนบวกเลขในชั้นอนุบาล เริ่มจากการนับ การบวกคือนับเพิ่ม เช่น วิธีหาคำตอบของ 5 + 3 คือนับต่อจาก 5 ไปอีก 3 นักเรียนหาผลบวกโดยนับ 6, 7, 8 ดังนั้นคำตอบของ 5 + 3 คือ 8 การหาผลบวกโดยการนับเป็นการสอนให้เข้าใจความหมายของการบวกเลข หากต้องการพัฒนาทักษะการบวกให้ได้คำตอบอย่างรวดเร็วจำเป็นต้องนำเทคนิคอื่นมาใช้แทนวิธีนี้ ถ้าไม่ใช้วิธีนับแล้วจะหาคำตอบได้อย่างไร ? ขอให้นึกถึงการพัฒนาทักษะการอ่านหนังสือของเรา เมื่อเริ่มเรียนหนังสือ เราถูกสอนให้สะกดเสียงตามตัวอักษร แล้วนำเสียงที่สะกดมารวมเป็นเสียงของคำ เมื่อเราเข้าใจวิธีสะกด และสะกดซ้ำ ๆ จนชำนาญ จากนั้นจะเกิดการพัฒนาอีกระดับหนึ่งที่สำคัญมากคือสามารถอ่านเสียงของคำนั้นได้ทันทีที่เห็นโดยไม่ต้องสะกด เช่น เมื่อเห็นคำว่า "กัด" เราอ่านออกเสียงได้ทันทีว่า กัด ถ้าสลับระหว่างตัว "ก" และ "ด" จะได้คำว่า "ดัก" ซื่งอ่านออกเสียงว่า ดัก เราสามารถอ่านออกเสียงได้ทันทีที่เห็นโดยไม่ต้องสะกด เพราะเราจำคำศัพท์นั้นทั้งคำ ไม่ใช่จำแค่ตัวอักษร แต่เราจำตำแหน่งการวางตัวอักษรด้วย นั่นคือเราจำคำศัพท์เหมือนเป็นสัญญลักษณ์ของเสียง ถ้าเราประยุกต์หลักการนี้กับการบวกเลข เมื่อเห็น 5 + 3 เราจะบอกคำตอบได้ทันทีว่า 8 เราจำ 5 + 3 เป็นสัญญลักษณ์แทนเลข 8 ซึ่งเป็นคำตอบของผลบวก เช่นเดียวกับที่เราจำศัพท์เป็นสัญญลักษณ์แทนเสียงของคำ เทคนิคนี้ทำให้เราหาผลบวกได้เร็วพอ ๆ กับการอ่านหนังสือโดยไม่ต้องสะกด การอ่านหนังสือโดยไม่ต้องสะกดเป็นเรื่องธรรมดาที่ทุกคนทำได้ ขอให้นึกย้อนกลับไปในอดีตว่าเราทำอย่างไรจึงสามารถพัฒนาความสามารถขึ้นมาได้ถึงระดับนี้ ตอนนี้เราจะย้อนกลับไปทำอย่างนั้นอีกครั้งแต่ไม่ใช่กับตัวหนังสือ แต่เป็นตัวเลข ถ้านำเลข 10 ตัว คือ 0-9 มาจับคู่บวกกัน 1 หลักจะได้คู่บวกทั้งหมด 10 X 10 = 100 คู่ ซึ่งใช้เป็นพื้นฐานของการบวกเลข ไม่ว่าจะบวกเลขกี่หลัก ก็คำนวณจากคู่บวกพื้นฐานนี้ เพราะการบวกเลขหลายหลัก ทำโดย บวกทีละหลัก เริ่มจากหลักขวาสุด (หลักหน่วย) ถ้าผลบวกเกิน 10 จะทดไปหลักถัดไป ทำเช่นนี้ไปเรื่อย ๆ จนครบทุกหลัก |
ไม่ต้องจำคู่บวกทั้ง 64 คู่ เพราะสามารถใช้เทคนิคบางอย่างช่วยดังนี้
|
| 3. | การบวกตัวเลขที่ต่างกันอยู่ 1 สามารถปรับให้เลขเท่ากันโดย +1 หรือ -1 แล้วคูณด้วย 2 จากนั้นชดเชยผลคูณด้วย - 1 หรือ +1 อีกครั้ง
| |||||||||||||||||||||||||||
| 4. | การนำเลข 9 ไปบวกกับตัวเลขอื่น ใช้เทคนิคทำให้เลข 9 เป็นเลข 10 ซึ่งช่วยให้การบวกเลขง่ายขึ้น
|
เหลือคู่บวกที่อยู่ในช่องสีขาวคือคู่บวกที่ต้องจำ ซึ่งมีเพียง 15 คู่ ในบรรดาคู่บวกเหล่านี้ขอเน้นคู่ที่ให้ผลบวกเป็น10 เพราะช่วยให้การบวกเลขง่ายขึ้น และช่วยให้การลบเลขเร็วขึ้นด้วย (ดูเทคนิคการลบเลขเร็วโดยใช้คู่บวกที่ให้ผลบวกเป็น 10 ) การจำคู่บวกเพียง 15 คู่เป็นเรื่องเล็กน้อยมาก เมื่อเทียบกับการจำคำศัพท์ในพจนานุกรมที่เราสามารถอ่านออกเสียงได้เกือนทุกคำโดยไม่ต้องสะกด เราสามารถจำคำศัพท์ได้มากมายเพราะเราใช้คำเหล่านั้นในชีวิตประจำวัน ทั้งพูด อ่าน เขียน ดังนั้นวิธีการที่ทำให้เราจำคู่บวกได้แม่นยำคือต้องเห็นคู่บวกเหล่านี้ทุกวัน และนำมาใช้บ่อย ๆ เหมือนการใช้ภาษาในชีวิตประจำวัน
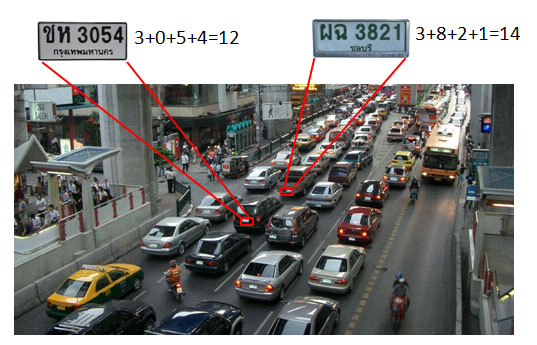
ใช้เวลาช่วงเดินทางบนท้องถนนฝึกบวกเลข โดยหาผลบวกของเลข 4 ตัวในทะเบียนรถ เช่น ทะเบียนรถ "สจ 5634" ผลบวกคือ 5+6+3+4 = 18 ในการฝึกห้ามใช้วิธีนับ เพราะวัตถุประสงค์การฝึกคือต้องการเลิกให้วิธีนับ ให้ใช้เทคนิคต่าง ๆ ที่กล่าวไว้ข้างต้น ขอให้ฝึกแบบสนุก โดยคิดว่ากำลังเล่นวิดีโอเกมไล่ยิงรถที่วิ่งอยู่บนท้องถนน กติกาของเกมคือหาผลบวกของเลข 4 ตัวในทะเบียนรถ ถ้าได้ผลบวกก่อนที่รถคันนั้นเคลื่อนที่ไปพ้นสายตาถือว่ายิงถูกเป้า แต่ถ้ามันเคลื่อนพ้นสายตาไปแล้วยังไม่ได้ผลบวกแสดงว่ายิงพลาดเป้า ขอให้เล่นเกมนี้ทุกวันที่เดินทางบนถนน เล่นจนจำผลบวกของตัวเลข 1 หลักได้ทุกคู่ เหมือนจำศัพท์ที่ใช้ในชีวิตประจำวันได้ทุกคำ
หลังจากฝึกบวกเลข 1 หลักจนชำนาญแล้ว ให้ฝึกบวกเลข 2 หลัก โดยแบ่งเลข 4 ตัวในทะเบียนรถ เป็นเลข 2 หลัก สองจำนวน แล้วนำสองจำนวนนี้บวกกัน เช่น 5634 = 56 + 34 = 90 เริ่มบวกหลักหน่วยก่อนคือ 6+4 =10 ได้ 0 ที่หลักหน่วยของคำตอบแล้วทด 1 ไปหลักสิบ ผลบวกของหลักสิบคือ 5+3 และบวกที่ทดไว้อีก 1 ได้ 9 ที่หลักสิบ คำตอบทั้งหมดคือ 90 เมื่อฝึกจนจำคู่บวกทุกคู่ได้อย่างแม่นยำแล้ว เราจะสามารถบวกเลขได้เร็วเหมือนอ่านหนังสือ
 |
| ที่มาภาพ http://www.mathsmethod.com/pic/speedup-add-practice.jpg |
ที่มาของข้อมูล http://www.mathsmethod.com/speedup-add.php
สมัครสมาชิก:
บทความ (Atom)






